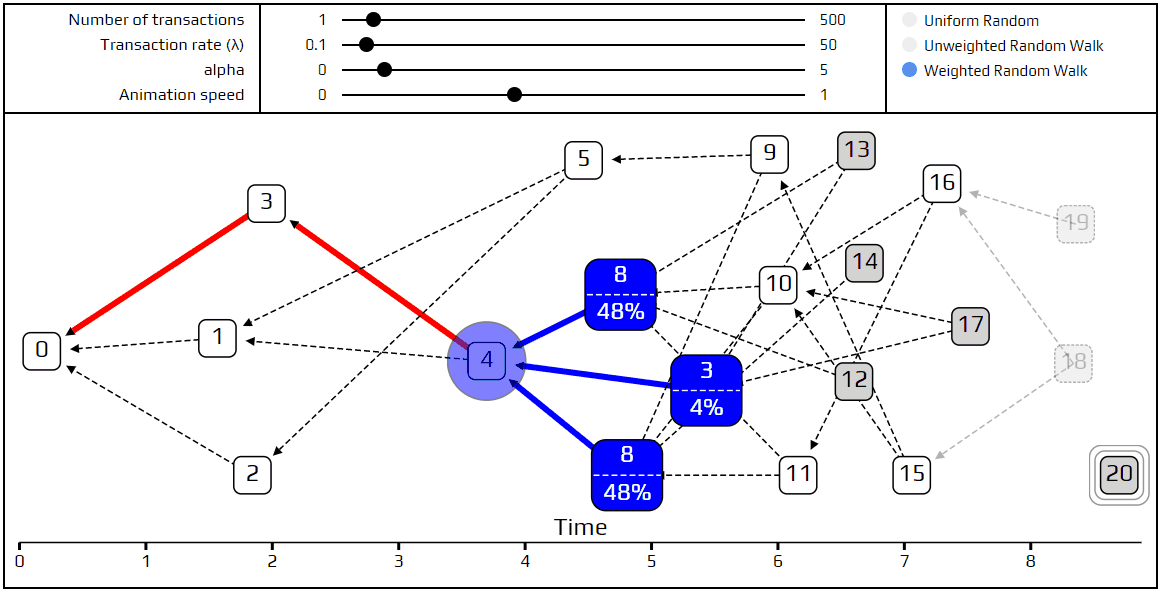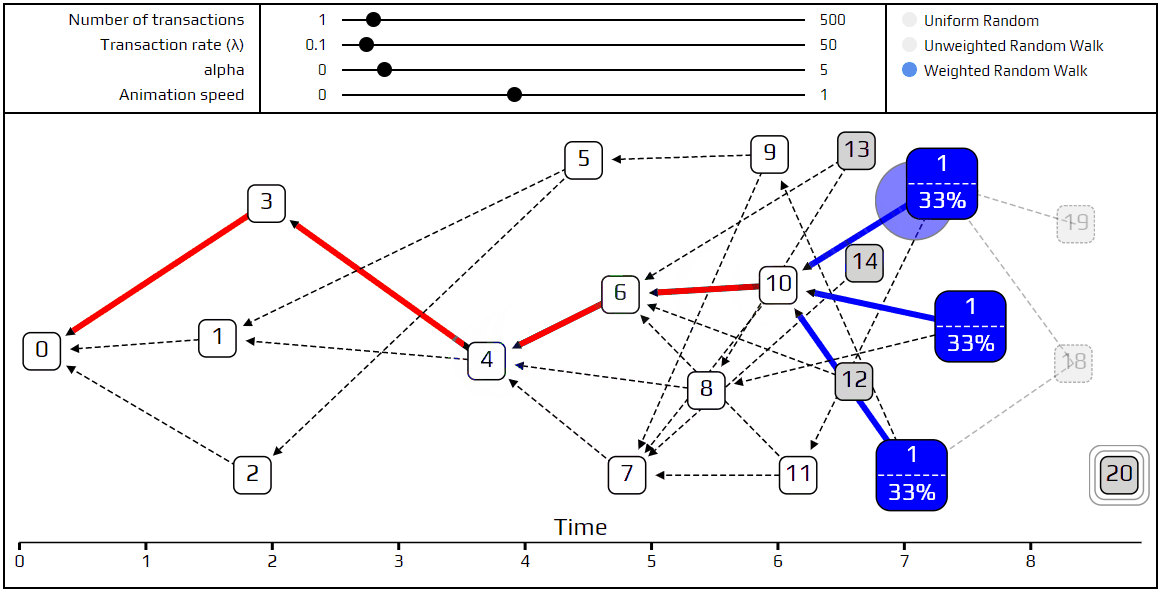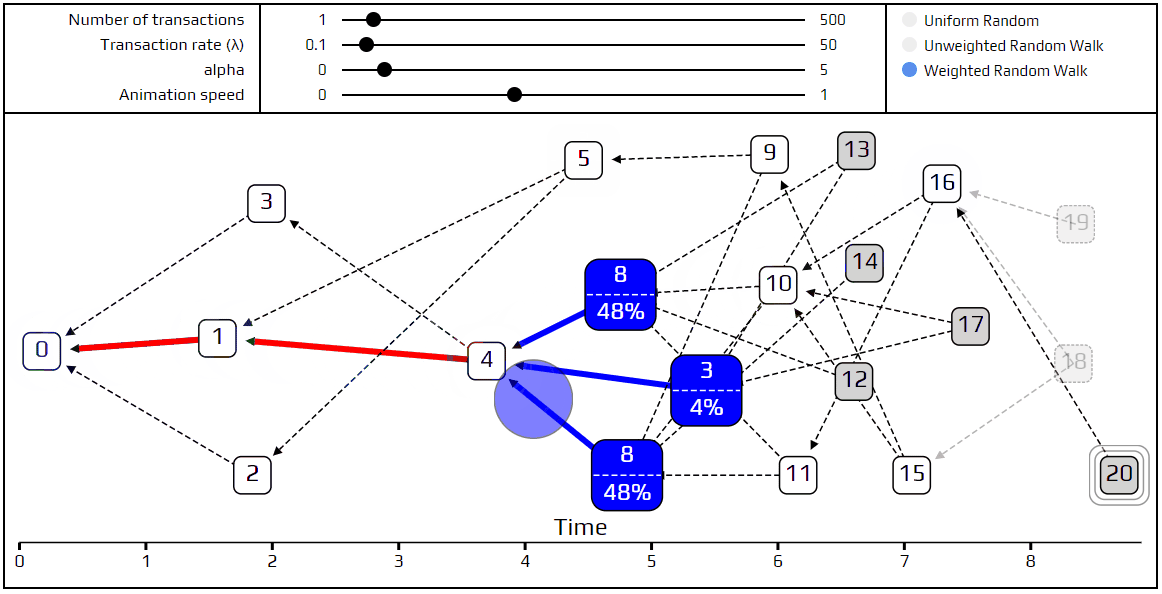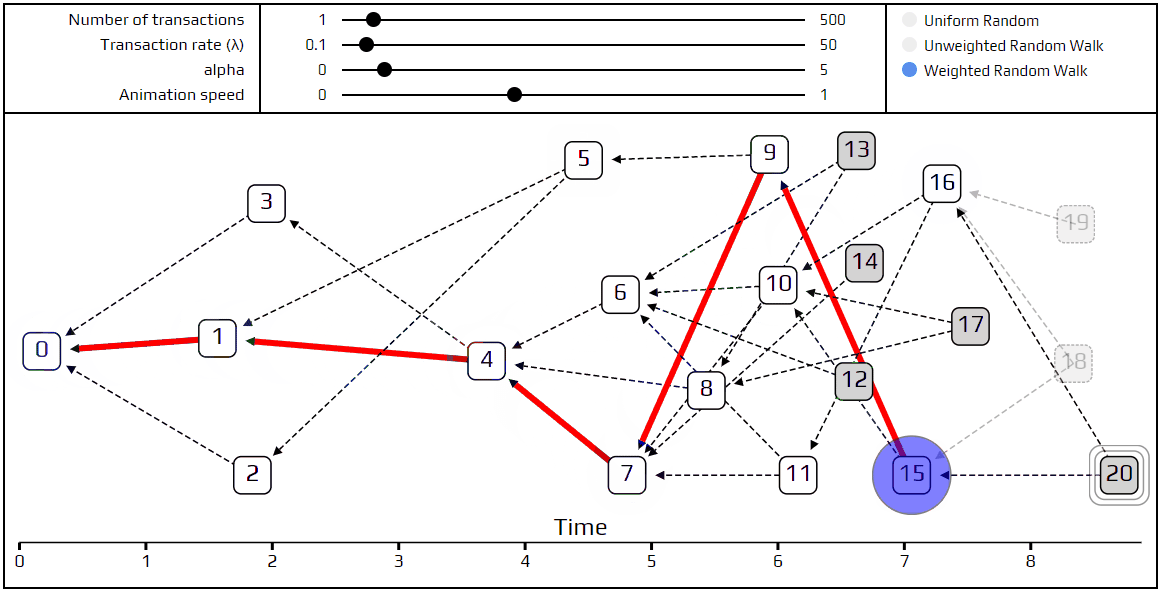
关于累积权重和加权的随机行走。
本文转载至:https://www.iotachina.com/tujiejieshaochanjiedi3bufenleijiquanzhonghejiaquandesuijixingzou.html

上周我们学习了不加权随机行走,今天我们将学习它更高级的用法:加权随机行走。
让我们先从它的功能目标开始学习。我们希望我们的tip选择算法功能之一是避免懒惰的tip。懒惰tip的特征是批准了以往的老旧交易,而不是最近发生的交易。因为它不需要与最新的缠结状态保持同步,所以它是懒惰tip,并且只在老旧数据的基础上广播自己的交易。这对网络没有帮助,因为没有新的交易事务被确认。
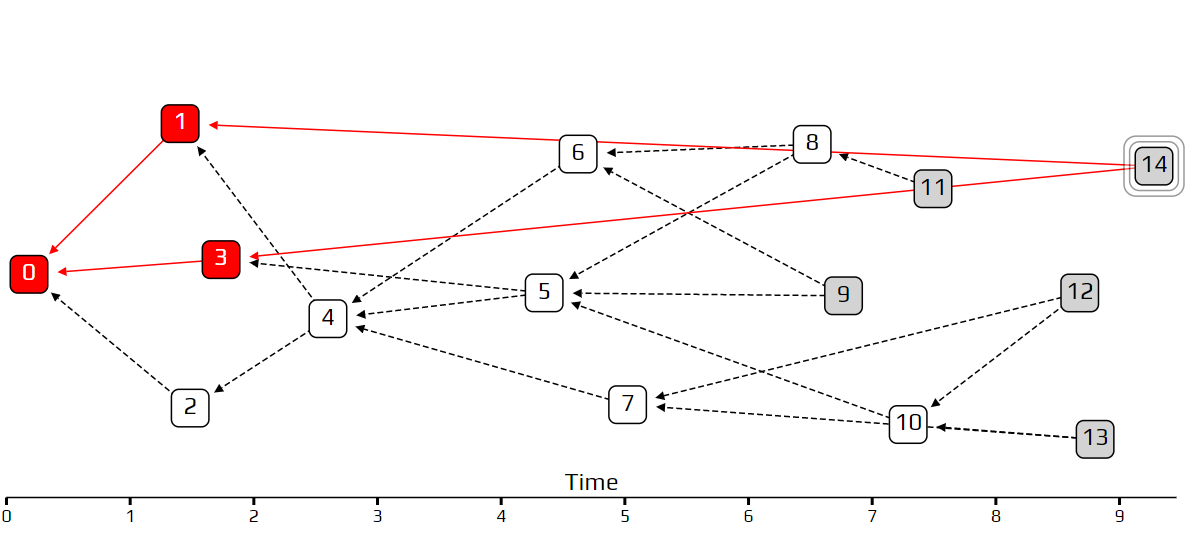
在上面的示例中,交易14是一个懒惰tip,它批准一些非常旧的交易事务。如果我们使用统一的随机tip选择算法,交易14就会与其他的交易同样的方式得到批准,所以它不会受到任何惩罚。使用不加权行走时,至少在这个例子中,这种不良行为甚至会被鼓励。
我们该如何处理这个问题?我们不能强迫参与者只批准最近的交易,因为这将与去中心化的想法相冲突。发起的交易应该能够批准任何人的请求。我们也没有可靠的方法来准确地说明每笔交易发起的具体时间,因此我们不能强制执行这样的规则。我们的解决方案是通过内建抵制这种行为的激励机制来构建我们的系统,这样懒惰的节点就不太可能得到其他人的认可。
我们的策略偏向于使用一种小概率选择懒惰tip的随机行走。我们将使用“累积权重”的概念来表示交易事务的重要性。我们更有可能走向一个高权重的交易而不是轻权重的交易。累积权重的定义非常简单:我们数出一笔交易事务有多少批准者,之后再加1。计数类型包括直接和间接批准。在下面的示例中,交易事务3的累计权重为5,因为它有4个交易事务可以验证了它(直接验证是5,间接验证是7、8和10)。
为什么它这样工作?让我们再看一个懒惰tip的情况。在下面的示例中,交易事务16是一个懒惰的tip。为了使交易16获得批准,随机行走点必须达到交易事务7,然后选择交易事务16而不是9。但这不太可能发生,因为交易事务16的累积权重为1,而交易事务9的累积权重为7!这是阻止懒惰行为的有效方法。
这时我们可能会问:我们是否需要随机性?我们可以发明超级加权随机行走,在每一个选择的关口都选择最高权重的交易,而不包含任何可能性。那么,我们会得到这样的结果:
超级加权行走——总是选择最高权重的交易示图。
灰色的方块是tip,零批准。虽然在图的右端有一些tip是正常的,但是如此多的tips在分散在时间轴上是一个问题。这些tips是遗留下来的交易事务,永远不会被批准。这就是tip选择算法偏离太远的负面因素:如果我们坚持在任何一个特定的点都选择最重的交易,那么很大一部分tip是永远不会被批准的。我们只剩下中心路径的批准交易,和被遗忘在场外tip。
我们需要一种方法来定义在特定的关口选择任何特定交易的可能性。我们选择的公式是否精确并不重要,只要我们偏向于具有较重交易权重的交易事务,并且有一个参数来控制这种偏向的程度即可。这里引出了我们的新参数α,即交易事务累积权重的重要系数。它的确切定义可以在白皮书中找到,如果有需求的话,将来我可以写一篇文章,介绍更多的细节。
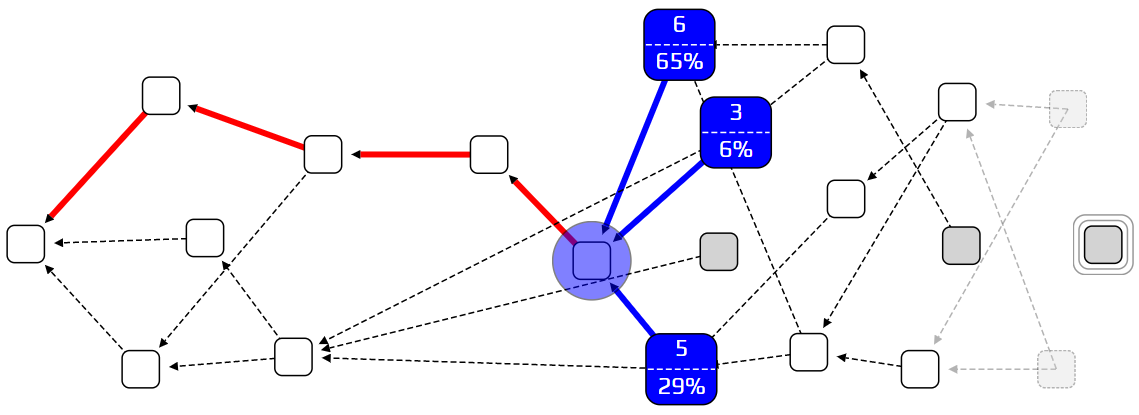
加权随机行走:每一个蓝色交易显示其累积重量,以及被选为下一步行走的概率。
如果我们将α设置为0,我们则回到未加权的行走。如果我们将α设置的非常高,我们会得到超级加权的行走。在这两者之间,我们可以在惩罚懒惰行为和不留下太多tip之间找到一个很好的平衡。确定一个理想的值在α值是非常重要的研究课题。
这种确定随机行走中每一步概率规则的方法称为马尔可夫链蒙特卡罗技术,即MCMC。在马尔可夫链中,每个步骤都不依赖于前一个步骤,而是遵循预先设定的规则。
一如既往,我们有一个模拟来展示这些新理念。我们建议调整α和λ的值,试试看你可以构造出什么样的有趣缠结。下周我们将详细讨论交易A批准交易B的含义,并定义交易事务于何时被确认。
by Covteam-Sma11_Tim3
生活不易,多才多艺。