

Sma11_Tim3's Studio.

Markov chain And Queuing theory

Sma11_Tim3's Studio.

Markov chain And Queuing theory

Blockchain

字数统计: 5.8k阅读时长: 23 min

 2020/12/02   Share

• 
• 
• 
• 
• 

马尔可夫链是随机过程中一种非常重要的统计模型，在研究中的应用十分的广泛，以下记录一些相关的知识点。

本文参考、转载至知乎https://www.zhihu.com/question/26665048

马尔可夫链（Markov Chain）

马尔可夫链是随机过程中的一个过程，一个统计模型。以实际的例子来描述：

假设我们家有一条小笨蛋，他每天中午12点的标配就是吃、玩、睡。永远就是三种状态中的一种，这就是所谓的状态分布。

那么你想知道他n天中午12点的状态吗？是在吃，还是在玩，还是在睡？这些状态发生的概率分别是多少？（知道你不想知道，就假装想知道吧~~为了学习，为了内卷）

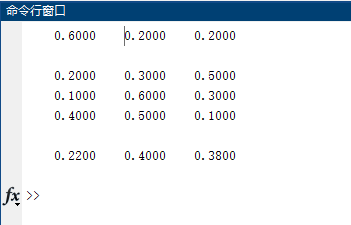
先看个假设，假定他的每个状态的转移都是有确定的概率的，比如今天玩，明天谁的概率是几，今天玩，明天也玩的概率是几，列出一个图表

这个矩阵就是转移概率矩阵P，并且它是保持不变的，就是说第一天到第二天的转移概率矩阵跟第二天到第三天的转移概率矩阵是一样的。（这个叫时齐，不细说了，有兴趣的同学自行百度）。

有了这个矩阵，再加上已知的第一天的状态分布，就可以计算出第N天的状态分布了。

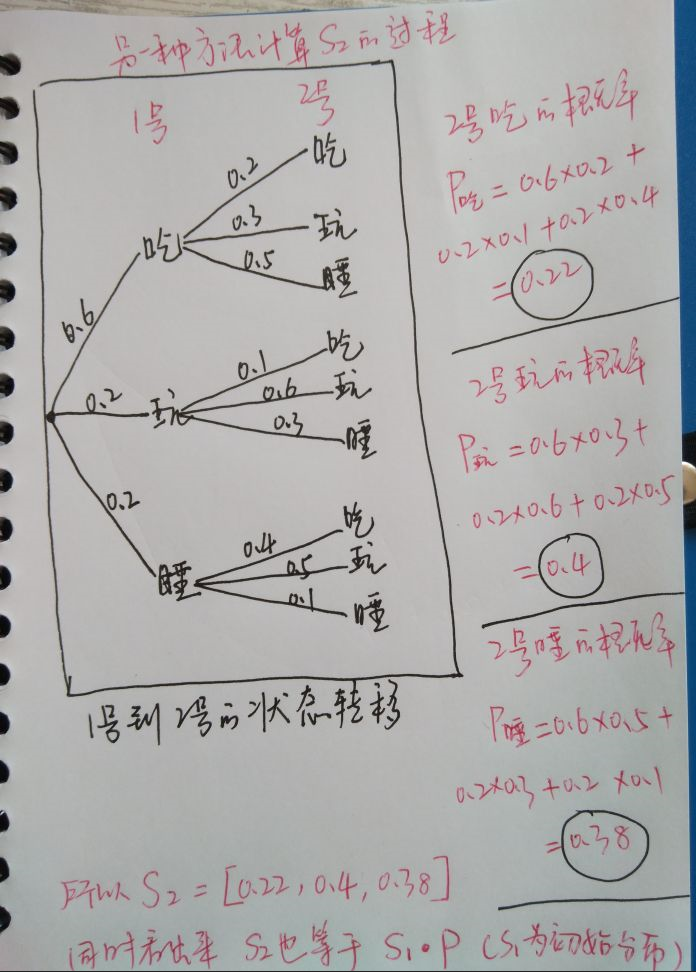
S1 是4月1号中午12点的的状态分布矩阵 [0.6, 0.2, 0.2]，里面的数字分别代表吃的概率，玩的概率，睡的概率。

那么

4月2号的状态分布矩阵 S2 = S1 * P (俩矩阵相乘)。

4月3号的状态分布矩阵 S3 = S2 P (*看见没，跟S1无关，只跟S2有关)。

4月4号的状态分布矩阵 S4 = S3 P (*看见没，跟S1，S2无关，只跟S3有关)。

…

4月n号的状态分布矩阵 Sn = Sn-1 P (*看见没，只跟它前面一个状态Sn-1有关)。

-————————————————————————————————————————————————————————————

总结：马尔可夫链就是这样一个任性的过程，它将来的状态分布只取决于现在，跟过去无关！

就把下面这幅图想象成是一个马尔可夫链吧。实际上就是一个随机变量随时间按照Markov性质进行变化的过程。

S2的计算过程可以利用MATLAB来进行计算，或者用另一种方法手动计算。

%% 方程组求解
clc;
clear;
B = [0.2 0.3 0.5;
     0.1 0.6 0.3;
     0.4 0.5 0.1];
% 定义一个3行3列的矩阵A，行与行之间使用分号隔开，每一行之间的元素使用空格隔开
A = [0.6 0.2 0.2]; %定义矩阵B
disp(A);disp(B); %显示A和B
X = A*B;
disp(X)

从马尔可夫链看矩阵的乘法

文章节选自橘子老君的知乎回答。https://www.zhihu.com/question/26665048/answer/551925518

问题

如下图所示的迷宫共有9个格子，相邻格子有门相通，9号格子就是迷宫出口. 整个迷宫将会在5分钟后坍塌. 1号格子有一只老鼠，这只老鼠以每分钟一格的速度在迷宫里乱窜（它通过各扇门的机会均等）。求此老鼠在迷宫坍塌之前逃生的概率。如果这只老鼠速度提高一倍，则老鼠在迷宫坍塌之前逃生的概率能增加多少？

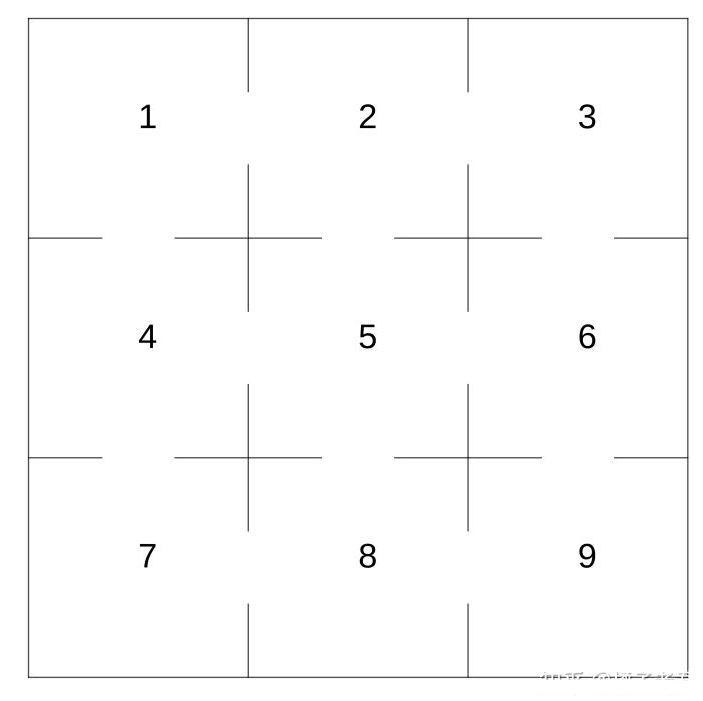
以上是2018年上海应用数学知识竞赛的一道初赛试题，橘子老君将会讲解如何用矩阵乘法来解决这个问题.

简化版问题

首先，我们不妨先把问题简化为一个4个格子的迷宫，老鼠仍以每分钟一格的速度在迷宫里乱窜，4号格子是迷宫的出口.

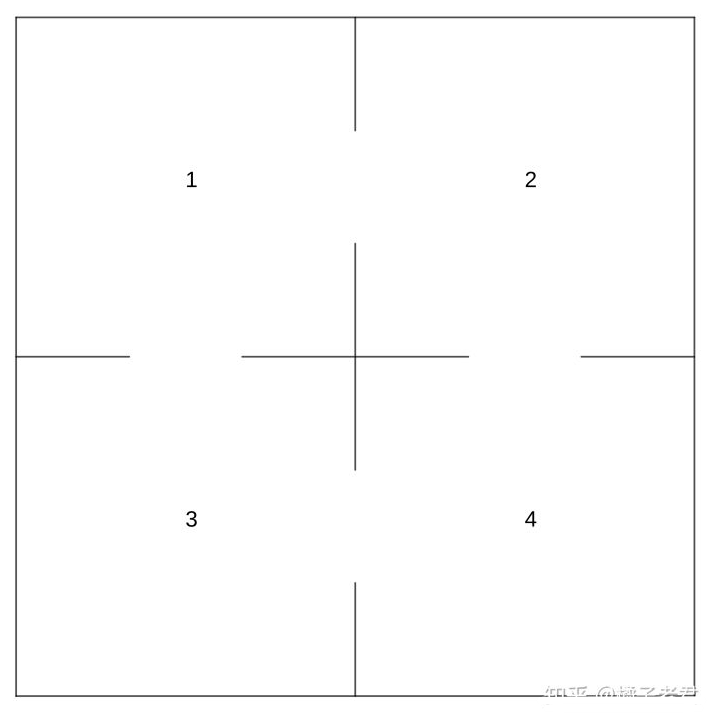
由通过各扇门的机会均等，可得格子之间转移的概率如图（由于4号格子是出口，所以老鼠到达四号格子后不会向其他格子转移），

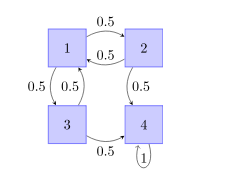
那么，老鼠经过一次移动，1分钟后在1-4号的格子的概率分别为0、0.5、0.5、0。

我们不妨用向量$v_n$表示n分钟后老鼠在1-4号的格子的概率，故$v_1=(0,0.5,0.5,0)$

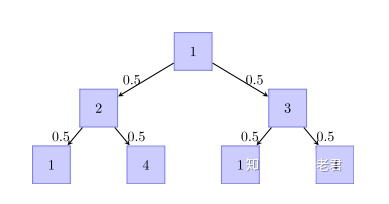
如上图，通过列举每一条路径，当老鼠经过两次移动，我们发现老鼠可能落在1号或4号格子.

考虑落在1号格子的情况，其对应有两条路径，$1\rightarrow2\rightarrow1$和$1\rightarrow3\rightarrow1$

那么根据老鼠每次的移动相互独立和加法原理，我们得到老鼠落在1号格子的概率为

$0.50.5+0.50.5=0.5$

同理可得落在2号格子的概率也为0.5，故$v_2=(0.5,0,0,0.5)$

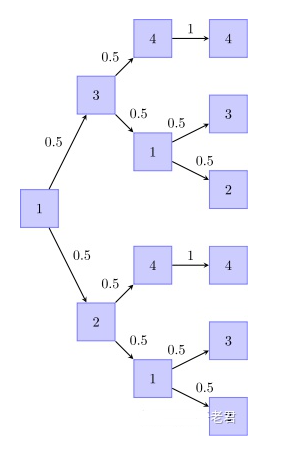
如上图，进一步列举3分钟后的每一条路径，考虑落在3号的格子的情况，对应的路径有两条$1\rightarrow2\rightarrow1\rightarrow3$和$1\rightarrow3\rightarrow1\rightarrow3$ . 通过分析格子间的转移概率不难得到，要使老鼠3分钟后落在3号格子，则2分钟后老鼠必须在1号格子. 故我们接下来将尝试写出相邻两分钟在不同格子概率的递推关系.

一般地，不妨用$v_n^{(i)}$表示n分钟老鼠落在$i$号格子的概率，则有：

$$\begin{aligned} &v_n^{(1)}=0.5\cdot v_{n-1}^{(2)}+0.5\cdot v_{n-1}^{(3)} \\ &v_n^{(2)}=0.5\cdot v_{n-1}^{(1)} \\ &v_n^{(3)}=0.5\cdot v_{n-1}^{(1)} \\ &v_n^{(4)}=0.5\cdot v_{n-1}^{(2)}+0.5\cdot v_{n-1}^{(3)}+1\cdot v_{n-1}^{(4)} \end{aligned}$$

由以上的递推关系，我们可以通过编程由计算机来完成计算：

#!/usr/bin/env python3
#coding=utf-8
n = 5  # 计算到n分钟后的情况
v = (1, 0, 0, 0)  # 0分钟后的情况
i = 0  # 当前计算到i分钟后
while i < n:
    v = (
        0.5 * v[1] + 0.5 * v[2],
        0.5 * v[0],
        0.5 * v[0],
        0.5 * v[1] + 0.5 * v[2] + v[3]
    )
    i = i + 1
    print('v' + str(i) + ': ' + str(v))

Output:

v1: (0.0, 0.5, 0.5, 0.0)
v2: (0.5, 0.0, 0.0, 0.5)
v3: (0.0, 0.25, 0.25, 0.5)
v4: (0.25, 0.0, 0.0, 0.75)
v5: (0.0, 0.125, 0.125, 0.75)

由上述结果，我们看到，老鼠在五分钟后逃出的概率为0.75.如果老鼠的移动速度翻倍那无非就是移动的次数从5次变为10次，得到逃出的概率为0.96875.

更一般的，我们可以用$a_{ij}$表示老鼠从$i$号格子向$j$号格子移动的概率，那么

$$v_n^{(i)}=a_{1i}\cdot v_{n-1}^{(1)}+a_{2i}\cdot v_{n-1}^{(2)}+a_{3i}\cdot v_{n-1}^{(3)}+a_{4i}\cdot v_{n-1}^{(4)}$$

即

$$v_n^{(i)}= \begin{pmatrix} a_{1i} \qquad a_{2i} \qquad a_{3i} \qquad a_{4i} \end{pmatrix} \begin{pmatrix} v_{n-1}^{(1)} \\ v_{n-1}^{(2)} \\ v_{n-1}^{(3)} \\ v_{n-1}^{(4)} \end{pmatrix}$$

故由矩阵乘法的定义，递推关系式可以写成：

$$\begin{pmatrix} v_{n}^{(1)} \\ v_{n}^{(2)} \\ v_{n}^{(3)} \\ v_{n}^{(4)} \end{pmatrix} = \begin{pmatrix} a_{11}&a_{21}&a_{31}&a_{41} \\ a_{12}&a_{22}&a_{32}&a_{42} \\ a_{13}&a_{23}&a_{33}&a_{43} \\ a_{14}&a_{24}&a_{34}&a_{44} \end{pmatrix} \begin{pmatrix} v_{n-1}^{(1)} \\ v_{n-1}^{(2)} \\ v_{n-1}^{(3)} \\ v_{n-1}^{(4)} \end{pmatrix}$$

马尔可夫链：一些定义

至此我们得到了解决此问题的矩阵形式,我们把此类在不同状态间随机移动的数学模型称为马尔可夫链. 老鼠在随机移动的过程中可能落在4个格子内，即存在4个状态. 而每做一次移动，其状态即发生转移. 为了讨论更一般的情况，我们不妨设有$m$种状态.

我们把经过$n$次转移后处于各个状态的概率所组成的向量$x_n$称为状态向量.$x_0$称为初始状态向量，

$$X_n= \begin{pmatrix} a_1 \\ ... \\ a_j \\ ... \\ a_m \end{pmatrix}$$

其中$a_j$表示经过$n$此转移后处于状态$j$的概率。

我们把各个状态之间转移的概率所组成的方阵$P$，称为转移矩阵，即

$$P=(p_{ij})_{m*n}$$

其中$P_{ij}$是状态$i$转移到状态$j$的概率。注意这里第$i$行第$j$列的元素是从状态$i$转移到状态$j$的概率.

那么同上文中的推导，我们可以得到相邻两个状态向量的关系，

$$x_{n+1}=Px_n,(n=0,1,2,...)$$

根据矩阵乘法的性质，不难推得$x_n=P^nx_0$

简化版问题的矩阵解法

在上文简化版问题中，

$$X_0= \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}, P= \begin{pmatrix} 0 & 0.5 & 0.5 & 0 \\ 0.5 & 0 & 0 & 0 \\ 0.5 & 0 & 0 & 0 \\ 0 & 0.5 & 0.5 & 1 \end{pmatrix}$$

故

$$X_n= \begin{pmatrix} 0 & 0.5 & 0.5 & 0 \\ 0.5 & 0 & 0 & 0 \\ 0.5 & 0 & 0 & 0 \\ 0 & 0.5 & 0.5 & 1 \end{pmatrix}^n \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}$$

下面我们用计算机来完成矩阵乘法计算：

#!/usr/bin/env python3
#coding=utf-8
import numpy as np
n = 5  # 计算到n次转移后的情况
i = 0  # 当前进行到i次转移
x = np.array([
    [1],
    [0],
    [0],
    [0]])  # 当前的状态向量
P = np.array([
    [0, 0.5, 0.5, 0],
    [0.5, 0, 0, 0],
    [0.5, 0, 0, 0],
    [0, 0.5, 0.5, 1]
])  # 转移矩阵
while i < n:
    x = P.dot(x)  # x=P*x
    i = i+1
    print('x'+str(i)+': \n'+str(x))

Output:

x1: 
[[0. ]
 [0.5]
 [0.5]
 [0. ]]
x2: 
[[0.5]
 [0. ]
 [0. ]
 [0.5]]
x3: 
[[0.  ]
 [0.25]
 [0.25]
 [0.5 ]]
x4: 
[[0.25]
 [0.  ]
 [0.  ]
 [0.75]]
x5: 
[[0.   ]
 [0.125]
 [0.125]
 [0.75 ]]

结语

相信掌握上文中简化版问题的解法后，那么原问题的求解也不过是按部就班而已了.

事实上对马尔可夫链的研究可以从以下几个角度进行：

• 若迷宫不会坍塌，则老鼠平均需要经过几分钟才能逃出迷宫？
• 若老鼠在进行足够多（无穷多）次移动后，是不是一定会逃出迷宫？
• 若迷宫并不存在出口，则老鼠在进行足够多（无穷多）次移动后，落在各个格子里的概率如何？

排队论

问题：排队过程是我们在生活中经常遇到的现象，例如去超市买东西、去医院看病常常需要排队。此时如果要求服务的数量超过服务机构（服务台、服务员等）的容量，到达的顾客不能够立即得到服务，因此出现了排队的现象。这种现象不仅出现在个人的日常生活中，通信中的占线问题、车站、码头等交通枢纽的阻塞，水客的存贮调节等都是有形或者无形的排队现象。

排队论（Queuing Theory）也被称作是随机服务系统理论，就是为了解决上述问题所发展的一门学科。主要的研究内容有三部分：

1. 性态问题，即研究各种排队系统的概率规律性，主要是研究队长分布、等待时间分布和忙期分布等，包括了瞬态和稳态两种情况。
2. 优化问题，又分为静态优化和动态优化，前者优化设计，后者优化现有排队系统的运行。
3. 排队系统的统计推断，即判断一个给定的排队系统符合与哪一种模型，以便根据排队理论进行分析和研究。

基本概念

凡是要求服务的对象统称为顾客，为顾客服务的人统称为服务员，由顾客和服务员共同组成了服务系统。对于一个服务系统来说，如果服务机构过于小，以至于不能够满足服务的众多顾客的需求，那么就会产生拥挤现象而使服务质量降低。因此顾客总是希望机构越大越好，但是机构过于大，人力物力等开销也会更大从而造成浪费。因此排队论模型的研究目的就是在顾客需要和服务机构的规模之间进行权衡决策，使其达到合理的平衡。

排队系统的组成和特征

一般的排队过程都由输入过程、排队规则、服务过程三部分组成

输入过程

输入过程是指顾客到来时间的规律性，可能有下列不同情况：

1. 顾客的组成可能是有限的，也可能是无限的。
2. 顾客到达的方式可能是一个—个的，也可能是成批的。
3. 顾客到达可以是相互独立的，即以前的到达情况对以后的到达没有影响； 否则是相关的。
4. 输入过程可以是平稳的，即相继到达的间隔时间分布及其数学期望、方差等 数字特征都与时间无关，否则是非平稳的。

排队规则

排队规则指到达排队系统的顾客按怎样的规则排队等待，可分为损失制，等待制和 混合制三种.

1. 损失制（消失制）。当顾客到达时，所有的服务台均被占用，顾客随即离去。
2. 等待制。当顾客到达时，所有的服务台均被占用，顾客就排队等待，直到接 受完服务才离去。例如出故障的机器排队等待维修就是这种情况。
   排队方式还分为单列、多列和循环队列。

服务过程

服务机构。主要有以下几种类型：单服务台；多服务台并联（每个服务台同 时为不同顾客服务）；多服务台串联（多服务台依次为同一顾客服务）；混合型。 （ii）服务规则。按为顾客服务的次序采用以下几种规则：

1. 先到先服务，这是通常的情形。
2. 后到先服务，如情报系统中，后到的情报信息往往有价值，因而常被优先处理。
3. 随机服务，服务台从等待的顾客中随机地取其一进行服务，而不管到达的先后。
4. 优先服务，如医疗系统对病情严重的病人给予优先治疗。

排队模型的符号表示

排队模型用六个符号表示，在符号之间用斜线隔开，即 X/Y/Z/A/B/C 。第一 个符号 X 表示顾客到达流或顾客到达间隔时间的分布；第二个符号Y 表示服务时间的 分布；第三个符号Z 表示服务台数目；第四个符号 A是系统容量限制；第五个符号B 是 顾客源数目；第六个符号C 是服务规则，如先到先服务 FCFS，后到先服务 LCFS 等。并 约定，如略去后三项，即指X/Y/Z/∞/∞/FCFS的情形。我们只讨论先到先服务 FCFS 的情形，所以略去第六项。
表示顾客到达间隔时间和服务时间的分布的约定符号为：
M —指数分布（M 是 Markov 的字头，因为指数分布具有无记忆性，即 Markov 性）；
D—确定型（Deterministic）；
Ek —k 阶爱尔朗(Erlang)分布；
G —一般（general）服务时间的分布；
GI —一般相互独立（General Independent）的时间间隔的分布。
例如，M/M/1表示相继到达间隔时间为指数分布、服务时间为指数分布、单服务台、等待制系统。
D/M/c/表示确定的到达时间、服务时间为指数分布、c个平行服务台（但顾客是一队）的模型。

排队系统的运行指标

为了研究排队系统运行的效率，估计其服务质量，确定系统的优参数，评价系统 的结构是否合理并研究其改进的措施，必须确定用以判断系统运行优劣的基本数量指标，这些数量指标通常是：

1. 平均队长：指系统内顾客数（包括正被服务的顾客与排队等待服务的顾客）的数学期望，记作Ls 。
2. 平均排队长:指系统内等待服务的顾客数的数学期望，记作 Lq 。
3. 平均逗留时间：顾客在系统内逗留时间（包括排队等待的时间和接受服务的时间）的数学期望，记作Ws 。
4. 平均等待时间：指一个顾客在排队系统中排队等待时间的数学期望，记作Wq 。
5. 平均忙期：指服务机构连续繁忙时间（顾客到达空闲服务机构起，到服务机构再次空闲止的时间）长度的数学期望，记为 Tb

排队模型的计算机模拟

确定随机变量概率分布的常用方法

在模拟一个带有随机因素的实际系统时，究竟用什么样的概率分布描述问题中的随 机变量，是我们总是要碰到的一个问题，下面简单介绍确定分布的常用方法：

【1 】根据一般知识和经验，可以假定其概率分布的形式，如顾客到达间隔服从指数分布 Exp(λ) ；产品需求量服从正态分布$N(\mu,\sigma^2)$；订票后但未能按时前往机场登机的人数服从二项分布 $B(n, p)$ 。然后由实际数据估计分布的参数 $\lambda,\mu,\sigma$ 等，参数估计 可用极大似然估计、矩估计等方法。

【2】 直接由大量的实际数据作直方图，得到经验分布，再通过假设检验，拟合分布 函数，可用$\chi^2$检验等方法。 3 o 既缺少先验知识，又缺少数据时，对区间(a,b) 内变化的随机变量，可选用 Beta 分布（包括均匀分布）。先根据经验确定随机变量的均值 μ 和频率最高时的数值（即密度函数的最大值点）m ，则 Beta 分布中的参数$\alpha_1,\alpha_2$可由以下关系求出：

$$\mu=a+\frac{a_1(b-a)}{a_1+a_2}, \qquad m=a+\frac{(a_1-1)(b-a)}{a_1+a_2-2}$$

计算机模拟

当排队系统的到达间隔时间和服务时间的概率分布很复杂时，或不能用公式给出 时，那么就不能用解析法求解。这就需用随机模拟法求解，现举例说明。

例1：设某仓库前有一卸货场，货车一般是夜间到达，白天卸货，每天只能卸货 2 车，若一天内到达数超过 2 车，那么就推迟到次日卸货。根据表 3 所示的数据，货车到 达数的概率分布（相对频率）平均为 1.5 车/天，求每天推迟卸货的平均车数。

解 这是单服务台的排队系统，可验证到达车数不服从泊松分布，服务时间也不服 从指数分布（这是定长服务时间）。 随机模拟法首先要求事件能按历史的概率分布规律出现。模拟时产生的随机数与事 件的对应关系如表 4。

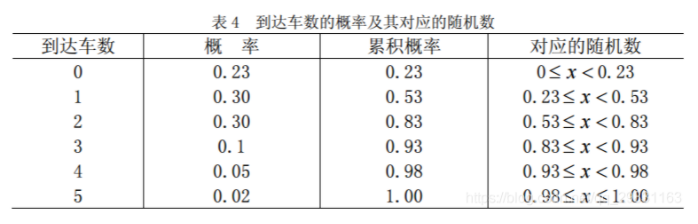
我们用 a1 表示产生的随机数，a2 表示到达的车数，a3 表示需要卸货车数，a4 表 示实际卸货车数，a5 表示推迟卸货车数。编写matlab程序如下：

clc
clear
rand('state',sum(100*clock));%定义一个随时间变化的初值，产生的伪随机数是确定的，产生的随机数会出现两次随机数一模一样的情况。
n=50000;
m=2;
a1=rand(n,1);
a2=a1; %a2初始化
%find函数，返回对应范围的位置
a2(find(a1<0.23))=0;
a2(find(0.23<=a1&a1<0.53))=1;
a2(find(0.53<=a1&a1<0.83))=2;
a2(find(0.83<=a1&a1<0.93),1)=3;
a2(find(0.93<=a1&a1<0.98),1)=4;
a2(find(a1>=0.98))=5;
%zeros(n,m)函数，生成n*m的零矩阵。
a3=zeros(n,1);
a4=zeros(n,1);
a5=zeros(n,1); %a2初始化
a3(1)=a2(1);
if a3(1)<=m
    a4(1)=a3(1);
    a5(1)=0;
else
     a4(1)=m;
     a5(1)=a2(1)-m;
end
for i=2:n
    a3(i)=a2(i)+a5(i-1);
    if a3(i)<=m 
        a4(i)=a3(i);
        a5(i)=0;
    else
        a4(i)=m;
        a5(i)=a3(i)-m;
    end
end
a=[a1,a2,a3,a4,a5];
answer=sum(a)/n

例2：银行计划安置自动取款机，已知 A 型机的价格是 B 型机的 2 倍，而 A 型机 的性能—平均服务率也是 B 型机的 2 倍，问应该购置 1 台 A 型机还是 2 台 B 型机。 为了通过模拟回答这类问题，作如下具体假设，顾客平均每分钟到达 1 位， A 型 机的平均服务时间为 0.9 分钟， B 型机为 1.8 分钟，顾客到达间隔和服务时间都服从指数分布，2 台 B 型机采取 M / M / 2 模型（排一队），用前 100 名顾客（第 1 位顾客到 达时取款机前为空）的平均等待时间为指标，对 A 型机和 B 型机分别作 1000 次模拟， 进行比较。

理论上已经得到，A型机和B型机前100名顾客的平均等待时间分别为$\mu_1(100)=4.13,\mu_2(100)=3.70$,即B型机优。

对于M/M/1模型，记第K位顾客的到达时刻为$c_k$，离开时刻为$g_k$，等待时间为$w_k$，它们很容易根据已有的到达间隔$i_k$和服务时间$s_k$按照以下的递推关系得到（$w_1=0$，设$c_1,g_1$已知）：

$$c_k=c_{k-1}+i_k,g_k=max(c_k,g_{k-1})+s_k$$ $$w_k=max(0,g_{k-1}-c_k),k=2,3,...$$

在模拟A型机时，我们用cspan表示到达间隔时间，sspan表示服务时间，ctime表示到达时间，gtime表示离开时间，wtime表示等待时间。我们总共模拟了m次，每次n个顾客。程序如下：

clear all;
clc;
tic%记录程序运行的时间
rand('state',sum(100*clock));
n=100;
m=1000;
mu1=1;
mu2=0.9;
for j=1:m
    cspan=exprnd(mu1,1,n);%R＝exprnd(MU，m，n)，生成服从参数为MU的m×n形式的指数分布的随机数矩阵。
    sspan=exprnd(mu2,1,n);
    ctime(1)=cspan(1);
    gtime(1)=ctime(1)+sspan(1);
    wtime(1)=0;
    for i=2:n
        ctime(i)=ctime(i-1)+cspan(i);
        gtime(i)=max(ctime(i),gtime(i-1))+sspan(i);
        wtime(i)=max(0,gtime(i-1)-ctime(i));
    end
    result1(j)=sum(wtime)/n;
end
result_1=sum(result1)/m 
toc

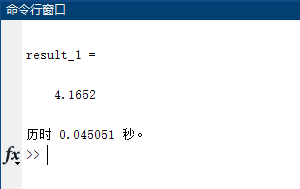
类似地，模拟 B 型机的程序如下：

clear
clc
tic
rand('state',sum(100*clock));
n=100;m=1000;mu1=1;mu2=1.8;
for j=1:m
    cspan=exprnd(mu1,1,n);sspan=exprnd(mu2,1,n);
    ctime(1)=cspan(1);ctime(2)=ctime(1)+cspan(2);
    gtime(1:2)=ctime(1:2)+sspan(1:2);
    wtime(1:2)=0;flag=gtime(1:2);
    for i=3:n
        ctime(i)=ctime(i-1)+cspan(i);
        gtime(i)=max(ctime(i),min(flag))+sspan(i);
        wtime(i)=max(0,min(flag)-ctime(i));
        flag=[max(flag),gtime(i)];
    end
    result2(j)=sum(wtime)/n;
end
result_2=sum(result2)/m
toc

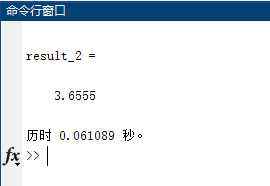
读者可以用下面的程序与上面的程序比较了解编程的效率问题。

clear
clc
tic
clear
rand('state',sum(100*clock));
n=100;m=1000;mu1=1;mu2=0.9;
for j=1:m
    ctime(1)=exprnd(mu1);
    gtime(1)=ctime(1)+exprnd(mu2);
    wtime(1)=0;
    for i=2:n
        ctime(i)=ctime(i-1)+exprnd(mu1);
        gtime(i)=max(ctime(i),gtime(i-1))+exprnd(mu2);
        wtime(i)=max(0,gtime(i-1)-ctime(i));
    end
    result(j)=sum(wtime)/n;
end
result=sum(result)/m
toc

原文作者：Sma11_Tim3

原文链接：http://yoursite.com/2020/12/02/Markov-chain-And-Queuing-theory/

发表日期：December 2nd 2020, 9:59:00 am

更新日期：December 28th 2020, 10:48:54 am

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

• Next Post
  MATLAB仿真模拟分布
• Previous Post
  MATLAB使用教程(九)

Powered by Hexotheme Archer

PV: :)

CATALOG

1. 1. 马尔可夫链（Markov Chain）
2. 2. 从马尔可夫链看矩阵的乘法
   1. 2.1. 问题
   2. 2.2. 简化版问题
      1. 2.2.1. 马尔可夫链：一些定义
   3. 2.3. 简化版问题的矩阵解法
   4. 2.4. 结语
3. 3. 排队论
   1. 3.1. 基本概念
   2. 3.2. 排队系统的组成和特征
      1. 3.2.1. 输入过程
      2. 3.2.2. 排队规则
      3. 3.2.3. 服务过程
   3. 3.3. 排队模型的符号表示
   4. 3.4. 排队系统的运行指标
   5. 3.5. 排队模型的计算机模拟
      1. 3.5.1. 确定随机变量概率分布的常用方法
      2. 3.5.2. 计算机模拟



• Archive
• Tag
• Cate

Total : 41

2021

• 11/10关于花指令
• 08/17Alpha：与随机性共舞
• 08/17图解介绍Tangle第2部分
• 08/17图解介绍Tangle第3部分
• 08/17图解介绍Tangle第1部分
• 08/17图解介绍Tangle第4部分
• 08/17图解介绍Tangle第5部分
• 03/04区块链常用术语汇总
• 03/04M/M/1/K单服务台混合制模型
• 03/01分布式账本之IOTA

2020

• 12/28共识算法之Tangle(缠结)
• 12/13攻防世界Reverse-Challenge-area
• 12/03ida动态调试elf(无坑详细)
• 12/02MATLAB仿真模拟分布
• 12/02Markov chain And Queuing theory
• 11/29MATLAB使用教程(三)
• 11/29MATLAB使用教程(七)
• 11/29MATLAB使用教程(九)
• 11/29MATLAB使用教程(二)
• 11/29MATLAB使用教程(五)
• 11/29MATLAB使用教程(八)
• 11/29MATLAB使用教程(四)
• 11/29MATLAB使用教程(六)
• 11/29MATLAB使用教程(一)
• 10/28计算机网络数学基础
• 10/14最大网络流(Maximum Network Flow)
• 10/14红黑树(Red Black Tree)
• 10/11Ipad搭建Vscode编程环境
• 09/25Blockchain笔记

2019

• 06/29Hello-Covteam
• 03/172018蓝桥杯总结

2018

• 12/27拜托教务系统强制评价
• 10/282018Covteam招新赛
• 10/2880x86汇编知识基础
• 10/28Pwntools使用简介
• 10/28Pwn入门笔记
• 10/28RSA
• 10/28网鼎杯第一场
• 10/28逆向入门基础汇编语言
• 10/28binwalk for windows
• 10/28Hello World

Covteam Algorithm Reverse Blockchain Daily gadgets MATLAB Pwn Crypto CTF



缺失模块。
1、请确保node版本大于6.2
2、在博客根目录（注意不是archer根目录）执行以下命令：
npm i hexo-generator-json-content --save
3、在根目录_config.yml里添加配置：

jsonContent:
  meta: false
  pages: false
  posts:
    title: true
    date: true
    path: true
    text: false
    raw: false
    content: false
    slug: false
    updated: false
    comments: false
    link: false
    permalink: false
    excerpt: false
    categories: true
    tags: true

