使用MATLAB来模拟具体的模型,依次介绍:泊松过程,指数分布,生灭过程。
泊松分布
日常生活中,大量事件是有固定频率的。
- 某医院平均每小时出生3个婴儿
- 某公司平均每10分钟接到1个电话
- 某超市平均每天销售4包xx牌奶粉
- 某网站平均每分钟有2次访问
它们的特点就是,我们可以预估这些事件的总数,但是没法知道具体的发生时间。已知平均每小时会来3个顾客,请问下一个小时,会到来几个顾客?
有可能一下子来6个,也有可能一个都不来。这是我们没法知道的。
泊松分布就是描述某段时间内,事件具体的发生概率。
概率函数:
等号的左边,P 表示概率,N表示某种函数关系,t 表示时间,n 表示数量,假如要表示一小时内来3个顾客的概率,就表示为P(N(1) = 3) 。等号的右边,$\lambda$表示事件的频率。
接下来两个小时,一个顾客都不来的概率是0.25%,基本不可能发生。
接下来一个小时,至少到来两个顾客的概率是80%。
泊松分布的示意图,可以用MATLAB得到相应的结果,代码如下:
1 | clear; |
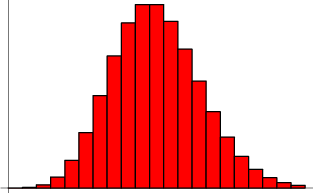
可以看到,在频率附近,事件的发生概率最高,然后向两边对称下降,即变得越大和越小都不太可能。每小时到达3个顾客,这是最可能的结果,到达人数越多或越少,就越不可能。
指数分布
指数分布是事件的时间间隔的概率。下面这些都属于指数分布。
- 婴儿出生的时间间隔
- 来电的时间间隔
- 奶粉销售的时间间隔
- 网站访问的时间间隔
指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间 t ,就等同于 t 之内没有任何婴儿出生。
反过来,事件在时间 t 之内发生的概率,就是1减去上面的值。
接下来15分钟,会有婴儿出生的概率是52.76%。
接下来的15分钟到30分钟,会有婴儿出生的概率是24.92%。
指数分布的MATLAB代码如下:
1 | clear; |
指数分布的图形大概是下面的样子。
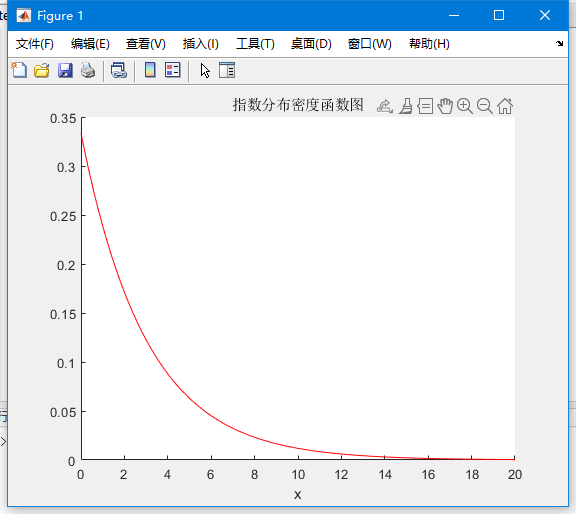
可以看到,随着间隔时间变长,事件的发生概率急剧下降,呈指数式衰减。想一想,如果每小时平均出生有3个顾客,上面已经算过了,下一个顾客间隔2小时才到来的概率是0.25%,那么间隔3小时、间隔4小时的概率,是不是更接近于0?
生灭过程
连续时间齐次马尔可夫链中一个特殊的分类,该分类过程状态的转移只允许从状态$j$到$j-1$或者$j+1$(如果这些状态存在)。这类随机过程非常适合描述队列中顾客的到达与离开过程,其中状态下标对应于等待服务的顾客数量。
具体的来说:如果在系统中的顾客数量为j,那么这个马尔可夫链就认为处于状态$j$。到达一个顾客,该过程转移到状态$j+1$,转移发生的速率为$q_{j,j+1}$。相对的顾客的离开使该过程从状态$j$移动到$j-1$,并且发生速率为$q_{j,j-1}$。具体公式
这两个式子为出生和死亡速率。这些速率可以是状态独立,但是由于该过程的齐次性,不能是时间独立的。同样根据定义,在状态$i$,对于除了取值$i,i+1,i-1$的所有$j$转移概率$q_{ij}$都为0。即:只有$q_{ii},q_{i,i+1},q_{i,i-1}$三个式子有取值,其余的式子取值均为0。另外根据以上的式子可以得出:
对于一个生灭过程,处于状态$j$有一个直观上的意义:人口数量为$j$,即排队系统中有$j$个顾客。一般来说,在状态$j$的时候,我们有一个顾客在接受服务并且有$j-1$个顾客在队列中等待服务。
生灭过程的平稳概率分布
因为生灭过程是一个各态历经的时间连续的马尔可夫链,它的平稳概率分布为:
用$π_j^*P_j$表示在状态$j$的平稳概率,并用以上的公式替代相关的变量可以得到以下的公式:
以矩阵形式表示,我们可以将前两个公式写为
其中
如果人口的规模有界限那么,这两个矩阵也是有限维的。定义$P(t)$如下:
最终可以将式子重写为:
矩阵Q被称为转移速率矩阵,研究生灭过程的第一步就是写出其Q矩阵。
注意到的是Q的对角线上的元素,即$q_{jj}$是离开状态$j$的概率值的负值。另外第$j$列中$q_{j-1,j}$比如($q_{01}$),表示从状态$j-1$到状态$j$的速率,相应的$q_{j+1,j}$比如($q_{32}$),表示从状态$j+1$到状态$j$的速率。其他所有的元素均为0。并且每一行所有元素加起来为0。