做区块链的实验分析的时候,需要使用MATLAB做仿真实验。记录一下相关的教程。本文章转载至https://blog.csdn.net/qq_38431572
前期回顾
上一期中,我们学了下面的知识:
- 定积分的基本概念和一些简单的几何意义。
- 使用 int 函数计算不定积分。
- 使用 int 函数计算定积分。
正文开始
多项式及其建立
在运算中我们经常接触到的就是所谓的多项式,比如很常见的一个多项式:$y=x^2+2x+3$
这里我们就说这是一个x的多项式,最高次是2次,常数项是3,二次项的系数是1,一次项的系数是2,相信这些大家都知道,就不再赘述了。
那么在matlab中,如何建立一个多项式呢?
通过系数建立多项式
如果在演草纸上,我们需要进行如下的步骤:
- 确定最高次项是几次。
- 确定各个次项的系数。
- 常数项是多少。
确定了上面的东西,就基本上可以确定一个多项式了,为了方便,我们使用程序表示这样一个多项式:$y=4x^4+3x^3+2x^2+x+1$,那么上述步骤在程序中是这样表示出来的:
1 | clc;clear; |
PS: 如果需要定义一个特殊的函数比如 $y=4x^4$ ,那么我们可以认为3次、2次、1次系数都为0,常数项也为0,写入数组即可。
上面的程序运行结果如图所示:
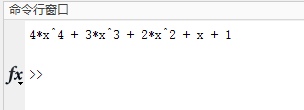
通过已知方程的根建立多项式
假设现在已有方程根:$x_1=1,x_2=4$ ,要求得到这个方程的式子,对于一元二次方程来讲,一个方法是:伟达定理,利用根与系数的关系,在matlab中,这种问题也可以得到解决,只需要一个函数即可:
1 | clc;clear; |
运行结果如图(我还不知道有没有可能求不出来这个对应方程,没试过哈哈哈哈,我猜应该是只要给出一套根,总能给出一个对应方程吧):

对多项式进行求导
求导即求多项式的导数,一般来讲,习惯上我们把 y = y(x) 对x求导函数直接简称为求导了,但是,我们求导时,一定要明确谁在对谁求导!!!在下文中,不做特殊说明的话,我们默认因变量是y,自变量是x,求导默认为 y对x求导,即求$\frac{dy}{dx}$。
使用matlab进行求导
多项式求导
代码如下:
1 | clc; clear; |
运行结果如图所示:

乘积求导
代码如下:
1 | %% 乘积求导 |
商求导
这个部分比较麻烦,商求导后返回值是有两个,因为很有可能出现求导后还是分数的形式,所以返回值是一个分子、一个分母,代码如下:
1 | %% 商求导 |
在商求导这个地方,所需要修改的仅仅是返回值而已,其他的地方几乎与乘积求导一致,还是很方便的。
运行结果如图所示:
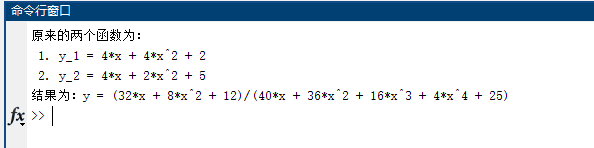
总结
今天我们学习了如下内容:
- 在matlab中使用已知系数、已知根简历方程多项式的方法。
- 求导的浅薄的基本概念。
- 在matlab中对多项式求导的一些函数,包括一些典型的求导类型:乘积求导、商求导等。
by Covteam-Sma11_Tim3
生活不易,多才多艺。