做区块链的实验分析的时候,需要使用MATLAB做仿真实验。记录一下相关的教程。本文章转载至https://blog.csdn.net/qq_38431572
前言
在第本系列第六篇/)中,我们讲解了一下相对来讲最普通的不定积分和定积分的问题,相信大家对积分已经有了大概的了解了,可是仍有一些小问题,比如如何计算多个变量的积分,比如二重积分、甚至三重三重积分呢?本讲中,我将做详细讲解。
本期内容
首先复习一下一元的定积分、然后讲解二重积分,如果可能,讲解三重积分。
复习定积分
在之前,先复习一下之前学习的内容。使用MATLAB求解定积分的步骤大概如下:
- 定义符号变量(syms关键字)
- 定义内联函数(inline函数)
- 使用MATLAB内置函数进行计算定积分或者不定积分(使用int函数,具体求解定积分还是不定积分,根据参数的数量决定)
我们都知道:定积分是求解一个图形与坐标轴围成的面积。而今天我们需要深入理解一下:定积分是求解两条曲线之间围成的面积,如果只有一个公式,比如$x$,我们可以理解成 $y=x$ 这个函数减去了 $y=0$这个常数函数,或者说,上面函数与x轴围成的面积减去了下面函数与x轴围成的面积(并且这个面积在x轴上方是正的,下方是负的),这样我们就可以推广,假设我们现在有两条曲线,一个是$sinx$,一个是$e^x$ ,我们求在$0-\pi$的范围内,两个图形围成的面积,容易知道,两个图形大概是这样围起来的:
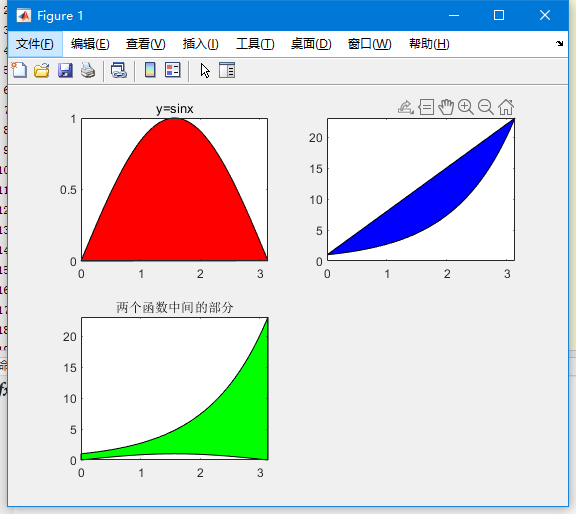
PS: 上图的代码和讲解如下
1 | %% 目标图像 |
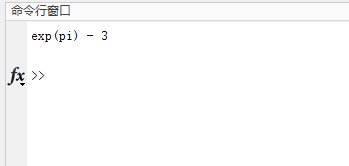
OK,那么我们就可以很容易的使用int()函数算出这样一个定积分,代码如下:
1 | %% 对上面的函数进行计算定积分 |
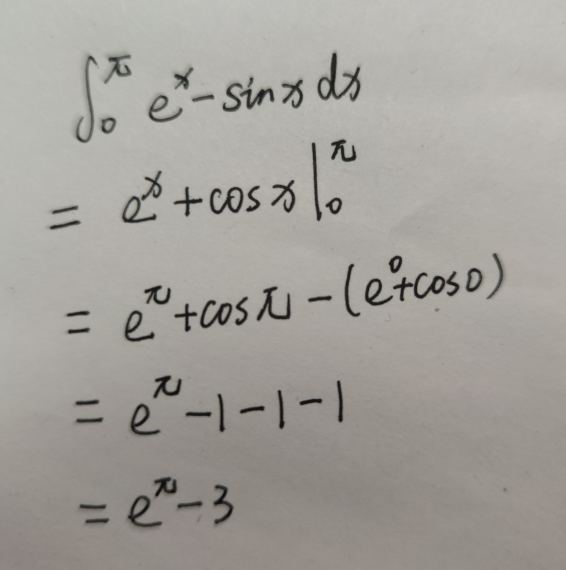
二重积分
关于二重积分的相关知识,大家自行下去学习吧。直接举出一个例子,假设底面如图所示(灰色阴影部分):
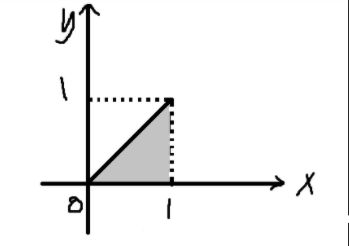
先积分x(Y型)时区域可表示为:$Dx=\{(x,y)|0<=y<=1, y<=x<=1\}$。
先积分y(X型)时区域可表示为:$Dy = \{(x,y)|0<=y<=x, 0<=x<=1\}$。
下面我们以X型为例,使用MATLAB计算曲面为$f(x,y) = xcos(y)$的曲顶柱体的体积:
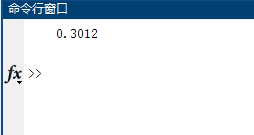
详细的代码以及注释见下方:
1 | %% 计算二重积分 |
最后,让我们欣赏一下这个曲面的形状吧:
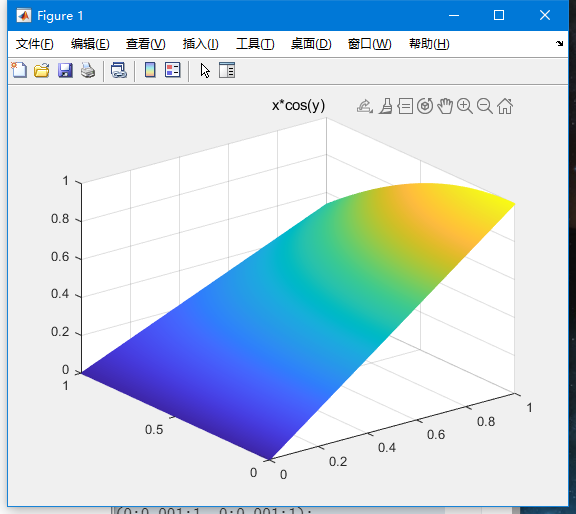
1 | %% 看一看这个曲面吧 |
今日小结
今天我们学到了如下的知识:
- 复习了之前学习的定积分、不定积分的内容
- 学习了二重积分的概念,以及应用的大概场景:求曲顶柱体体积,平面薄片质量(底面换位薄片,被积函数即薄片面密度的函数)等。
- 学会了如何在一个figure里面绘制多个图像
- 学会了如何在MATLAB中绘制图像、对目标区域填充颜色并命名标题
- 学会了怎么使用MATLAB的integral2计算二重积分
- 学会了怎么在MATLAB中声明(定义)一个函数句柄,或者说创建一个多元函数,以及怎么反解一个函数中某个变量(y = @(x) x ,此处函数是y=x),其实说白了,反解函数就是定义函数句柄。
- 学会了怎么在MATLAB中绘制二维曲面的图像。