做区块链的实验分析的时候,需要使用MATLAB做仿真实验。记录一下相关的教程。本文章转载至https://blog.csdn.net/qq_38431572
前期回顾
在上期教程中,我们学习了下面的知识点:
- 如何声明、定义、调用函数(文件)。
- 给函数传递参数、接受函数的返回值。
- MATLAB中矩阵的简单使用和下标索引。
- 给我们代码模块化。
- MATLAB中for循环(遍历)的使用。
- 如何从一个文件调用另一个函数文件。
本期目标
在数学中经常遇见的一个问题就是方程求解,特别是线性代数中,很经常遇见线性方程组的求解问题,今天就来用MATLAB来探讨线性方程组的求解问题。
正文
一般方程
一般来讲,我们看到的方程都是这个样式的:$ax=b$,其中$a、b$都是常数,很显然,这时候$x$的解就是$b/a$。
也就是说我们拿后面的值除以前面的系数,即可得到解$X$。
方程组(目前仅讨论方程个数和未知数个数一样的情况)
刚刚我们讲的是一般方程,那推广到线性方程组,假设我们现在有个这样的方程:
相信大家运用高中知识也能很快的求出这个方程的答案,但是,如果四阶?五阶甚至更高呢?不如转换为矩阵的方法。
根据线性代数的知识,我们可以得到这样一个增广矩阵:
那我们令系数矩阵是A,结果矩阵是B,这个解矩阵X该怎么算呢?
额外知识
此部分提供给还未学过线性代数的同学看,如果知道基本知识可以先行跳过。
上面的矩阵方程可以视为这样的矩阵方程:
其中,令X为未知数的矩阵,前面的三乘三的系数矩阵称为A,等号右边的结果矩阵称为B,方程组即可表述为:
AX = B,求X。
矩阵A的列数和矩阵X的行数相同时才可写成此种形式,因为当A的列数(这里是三列)等于X的行数(这里是三行)才能进行矩阵乘法运算。
矩阵乘法运算是这样的:
易看出:如果A是 n 行 m 列,则X需要是 m 行 s 列才可相乘,且结果矩阵必是 n 行 s 列。
所以按照上面的运算法则,我们就可以看出,矩阵方程和原来的方程组是等价的。
回到正文
我们已经得到了方程组对应的矩阵方程$\left[ \begin{matrix} 4 & 1 & -2 \\ 2 & 2 & 1 \\ 3 & 1 & -1\end{matrix} \right]\left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right]=\left[ \begin{matrix} 1\\ 2\\ 3\end{matrix} \right]$
那么编程的第一件事就应该是在程序里面表述这个方程组。下面看代码:
1 | %% 方程组求解 |
现在我们便可以在程序中得到两个矩阵,分别是A和B,定义的时候也可以不换行,但是换行定义看起来毕竟方便、易读。
运行代码就能看到我们定义的这两个矩阵:
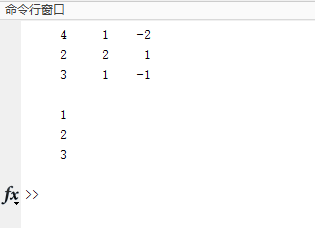
同样,我们也可以在右边的工作区查看我们的这两个变量:
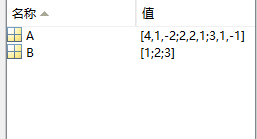
还可以双击其名称查看详细的信息。
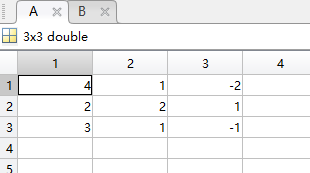
现在,我们得到了两个矩阵,万事俱备,只欠东风,我们现在只需要一个除法即可得出这个解矩阵X。
现在在最后面加入这个代码:
1 | X = A\B; % 左除 |
可能会有些人觉得奇怪,怎么A在左边并且这个写的是斜杠呢?
如果我们学习过矩阵便知道,矩阵的乘法是没法前后调换的,即 AB 不等于 BA,也就是说,AX = B,要求这个X,我们需要在两边的左边同时除以A(严谨说法叫做乘以A的逆矩阵),即 1/A A X = 1/A B,也叫做左除,而在MATLAB中,左除符号就是这个“ \ ”符号,所以应这样使用,即 A \ B代表 1/A B(严谨来说,就是A的逆矩阵*B),即可得到X。
运行后我们便可看到解矩阵的结果:
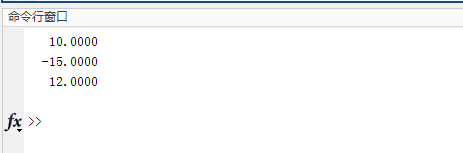
左除和右除
上面讲的是左除,下面我们来说说右除,也就是在右边乘以1/A(严谨说法叫做A的逆矩阵),那么这个方程组应该是这样的:
$XA=B$
如果A和B不变的话,对应的矩阵应该是这样的:
然后根据乘法的运算法则,可以发现,这个方程是没法解的(因为根本就没法乘,前面矩阵1列,后面矩阵3行,不相等,没法进行乘法运算)
所以,如果进行这样的乘法运算,我们需要把X的解矩阵变换(注意,变换后乘出来的结果和之前的方程组不一样,不一样!):
那么根据运算律,我们可以得到现在的方程组是:
那么这个X如何求呢?
根据原方程: XA = B,我们需要在等号两端的右边同时乘以 1/A(严谨来说是A的逆矩阵),即:
X A 1/A = B 1/A(左右千万不能放错) ==> X = B1/A
在代码中,右除是这样写的(注意代码改动,因为矩阵B变了):
1 | %% 方程组求解,右除 |
然后运行:
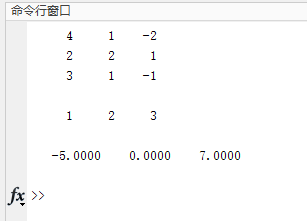
总结
今天我们学习了如下的知识:
- 在MATLAB中定义矩阵。
- 线性代数矩阵乘法运算、求解知识。
- 关于矩阵乘法左除、右除的区别。
- 在MATLAB中求解两种矩阵方程的方法。
by Covteam-Sma11_Tim3
生活不易,多才多艺。