做区块链的实验分析的时候,需要使用MATLAB做仿真实验。记录一下相关的教程。本文章转载至https://blog.csdn.net/qq_38431572
前言
在上一篇文章中,我们学习了
- 在matlab中对外输出
- 格式化字符串
- 在文件中编写
- 调整matlab的字符编码格式
- 编写代码时的一些小提示
本讲开始
计算一元二次方程
这一讲我们以科学计算开始,使用matlab计算精确度很高,我们可以尝试来计算一下黄金分割率(定义大家可以自行百度一下,这里就不再说了):
计算黄金分割率的公式是:$\phi=\frac{\sqrt 5\pm1}{2}$
如果使用加法,得到的是1.618……..,如果使用减法,得到的是0.618……..,这两个结果都是正确的。因为他们两个只相差1.
首先,我们把这个公式转化一下,把根号去掉,转化为一个一元二次方程:
(因为+号时无解,所以舍去)然后我们就只需要使用matlab解开这个方程了!
1 | clear; |
结果如下:
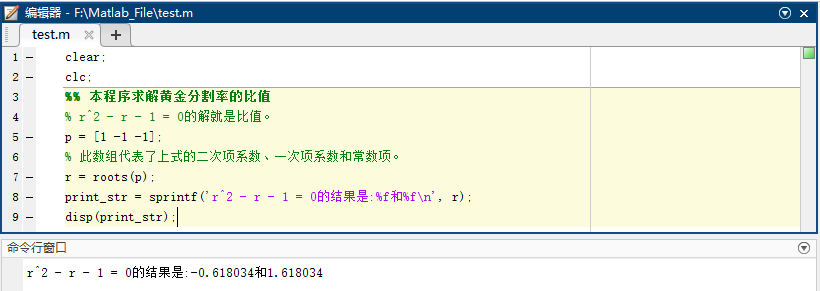
可以看到,这两个数就是我们需要的结果了。
当然,如果我们实现不知道各个系数,只知道我们的公式(假设),我们可以使用solve函数来计算,可以大大节省我们的时间:
1 | %% 第二种计算的方法。 |
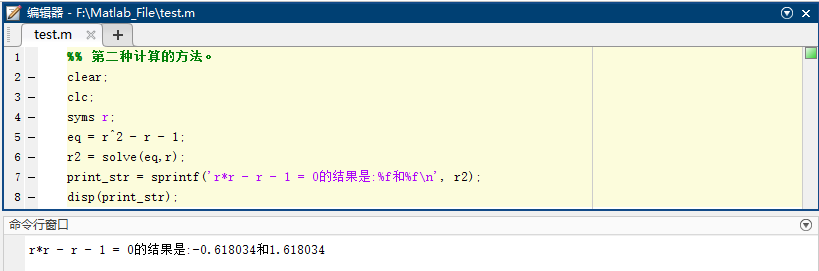
同样也能得到我们想要的结果,但同时注意:占位符是 %f 千万不能写成其他的。
但是你可能觉得这个精确度不高,没问题,使用 vpa 方法可以提高精确度到很多位!!
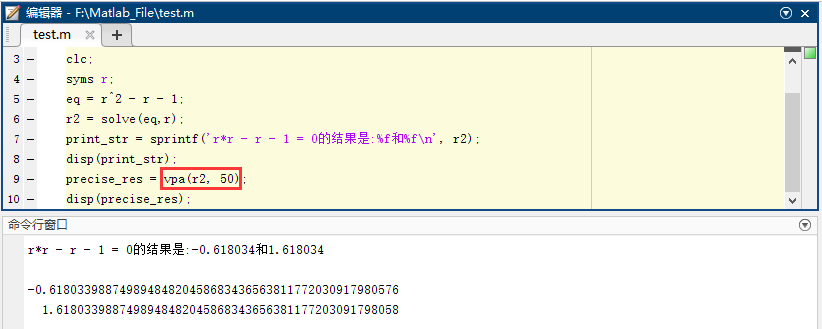
第一个参数是我们的数据,第二个参数是我们精确到小数点后的位数。可以得到很多位的结果(好像理论是无限,但是前提是电脑的CPU够厉害并且你有足够的耐心并且你的内存够大!!在我的电脑上,计算到小数点后五万位已经有明显的一秒左右延迟了。)
看一元方程的图形
上面我们计算了这个方程,大家知道,在数学中,一元二次方程的表现是开口向上或者向下的抛物线,方程的解就是与X轴的交点(即零点)。
那么如何在matlab中表现呢?下面上代码!
1 | %% 显示函数的图像 |
运行我们就能得到我们想要的东西:
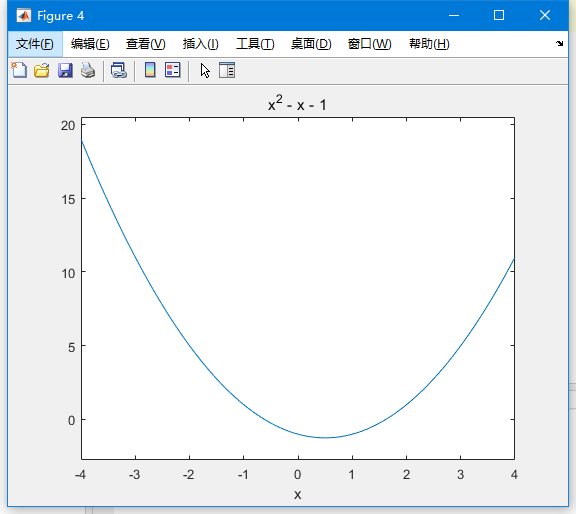
大家可以看到,在 x = 0 的水平线处有我们的两个x的值。
小疑问?
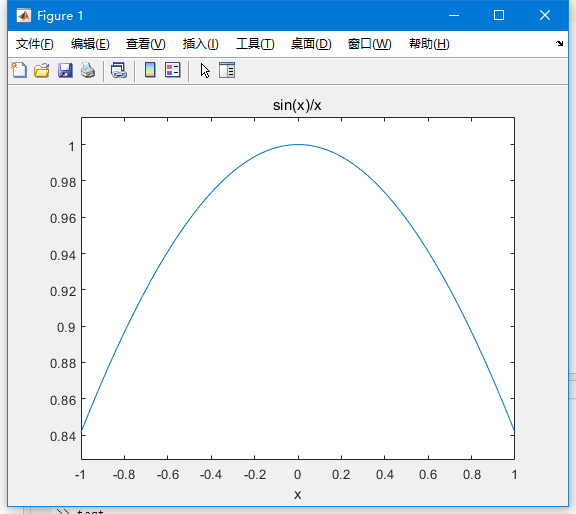
加入我们写成另一个形式呢(1/x - (x - 1))?很容易知道,这俩图像虽然图形不一样,但是也是黄金分割率公式的变形,只需移项消元即可得到这个形式,很明显,这个世子有个点是不存在的(点0,不能为分母),这个公式的图形也明显类似于反比例函数(在点0处的间断点是第二类间断点,0+0处是正无穷大,0-0处是负无穷大)。
这个没问题!matlab会计算我们需要的函数图形,有间断点会计算极限,尽可能的满足我们(这次我们在代码里标出这个解的位置),代码如下:
1 | %% 第二种形式 |
而图形,如同我们预期,显示出了一个双曲线,并且在零点处标出了我们的符号:
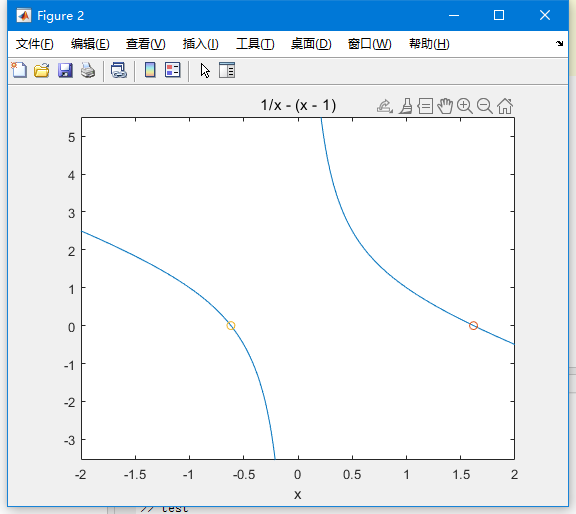
计算 sinx/x 的0处的比值。我们知道,当x->0的时候,sinx 和x是等价无穷小,比值是1,那么,我们看一下图形把!
那么这个图形的函数,大家自己解决哦!!
今日总结
我们今天学习了如下知识点:
- 使用roots函数求一元二次方程的根。
- 使用solve函数求方程的根(注意哦,没说是几次的。大家可以试试三次函数等,甚至没实数根的大家也可以试试,我们要从认识得到实践,然后再根据实践得到新的认识!)
- 使用inline函数和ezplot函数一起绘制函数图形(小技巧:ezplot音似:easy plot,简单绘制,方便我们记忆)
- 使用 fzero 函数和 plot 函数绘制某一点处的零点。
by Covteam-Sma11_Tim3
生活不易,多才多艺。